어린 남동생 Ike 를 위해 선물을 사려고 한다 . 그러나 Ike 는 선물에 대해 아주 특이한 취향이 있다 .
Ike 는 특정 형태로 구성 된 선물 만을 좋아한다 . 한 가게에서 모빌을 팔고 있는 것을 발견하였다 .
모빌은 여러 층으로 구성된 장식으로 보통 천정에 매달아 놓는다 .
각각의 모빌은 수평인 막대들이 아래 그림과 같이 줄로 매어져 있는 것이다 .
각 수평 막대의 양 끝에 줄이 매어 있으며 , 이 줄은 또 다른 수평 막대에 묶여 있거나 아니면 장난감이 묶여 있다 .
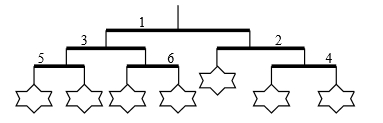
아래의 그림은 모빌의 한 예를 보여 준다 :

동생 Ike 를 만족 시키기 위하여 , 다음과 같은 제약 조건을 만족하도록 구성을 바꿀 수 있는 모빌을 찾아야 한다 :
(i) 모든 장난감은 같은 레벨에 매달려 있거나 또는 임의의 두 장난감이 같은 레 벨이 아니라면 레벨의 차이는 1 이다 .
( 장난감의 레벨이란 천정까지 연결된 수평 막대의 수를 일컬은다 .)
(ii) 만일 두 개의 장난감이 매달린 레벨이 다르다면 , 왼쪽에 있는 장난감이 오른 쪽의 장난감보다 아래에 있어야 한다 .
모빌 들은 막대의 양끝의 줄을 바꾸어 매어 구성을 바꿀 수 있다 . 이는 막대 의 왼쪽과 오른쪽 끝에 매어 있는 줄을 풀어
반대쪽 끝에 ( 즉 , 각각 오른쪽과 왼쪽 끝에 ) 다시 매어 놓으면 된다 .
이런 작업은 그 밑에 매달려있는 막대나 장난감의 구성 을 변화시키지는 않는다 .
여러분들은 정보올림피아드를 위하여 훈련하여 왔으므로 ,
단련한 실력을 발휘하여 주어진 모빌이 Ike 가 좋아하는 선물이 되도록 구성을 바꿀 수 있는지를 결정하는 알고리즘을 설계하여라 .
예로서 , 앞의 그림에 주어진 모빌을 고려하여 보자 . Ike 는 이 모빌을 좋아하지 않을 것이다 .
이 모빌은 제약조건 (i) 을 만족하지만 조건 (ii) 는 만족하지 못한다
가장 왼쪽 끝에 있는 장난감이 오른쪽에 있는 장난감들 보다 높은 레벨에 놓여있다 .
그러나 이 모빌은 Ike 가 좋아하는 모습으로 바꿀 수 있다 . 아래와 같이 바꾸면 된다 .
1. 우선 1 번 막대의 양쪽 끝을 서로 바꾼다 . 이런 바꿈으로 2 번 막대와 3 번 막대의 위치가 바뀌게 되어 , 그 결과는 아래의 그림과 같이 된다 .
2. 그 다음으로 , 2 번 막대의 양쪽 끝을 서로 바꾼다 . 이렇게 하면 4 번 막대가 2 번 막 대의 왼쪽 끝으로 , 장난감은 오른쪽 끝으로 옮겨지게 된다 .

이 결과는 Ike 가 좋아하는 구성이 된다 . 모든 장난감들 이 매달린 레벨의 차이 는 많아야 1 이며 ,
아래 레벨에 있는 장난감들은 위 레벨에 있는 장난감들 보다 모두 왼쪽에 위치하고 있다 .
여러분들이 수행하여야 할 작업은 주어진 모빌에 대하여 , Ike 가 좋아하는 모습으로 다시 구성하려고 할 때 ( 만일 가능하다면 ),
막대의 양쪽 끝의 줄을 서로 바꾸 어 매는 작업의 최소 회수를 결정하는 것이다 .