문제1.
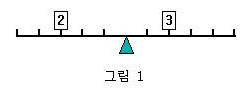
무게가 서로 다른 추들의 집합이 주어진다. 각 추의 무게는 1g 이상 9g 이하의 정수이다. 이 추들 중에서 몇 개를 선택하여 양팔저울에 올려서 평형을 만들고자 한다. 양팔저울에는 양쪽에 5개씩 등간격의 눈금이 표시되어 있고 추는 눈금 위에만 놓일 수 있다. 한 눈금 위에는 하나의 추만이 놓일 수 있다. 예를 들어, {2, 3, 4, 5, 9}가 추의 집합으로 주어졌을 때, 아래 그림 1과 같이 왼쪽에는 2g짜리 추를 중심에서 3 떨어진 자리에 놓고, 오른쪽에는 3g짜리 추를 중심에서 2떨어진 자리에 놓으면 저울은 평형을 이루게 된다.(2*3 = 3*2)
위와 동일한 추 집합에서 아래 그림 2와 같이 양쪽에 서로 다른 수의 추를 배치해서 평형을 이룰 수도 있다. (4*4 + 5*2 = 5*4)

그림 1, 그림 2와 같이 저울이 평형을 이룬 경우 추가 놓인 모양에 따라 대응되는 하나의 숫자를 다음과 같이 생성한다. 추가 놓이지 않은 빈 눈금에는 0이 들어가고 추가 놓인 눈금은 그 추의 무게에 해당하는 숫자가 들어간다. 단, 이렇게 만들었을 때 0이 아닌 첫 숫자가 나타나기까지의 왼쪽에 있는 모든 0은 제거한다. 예를 들면, 그림 1에 대응되는 숫자는 20003000이 된다. 그림 2에 해당되는 숫자는 402000050이다. 이렇게 하면 양팔저울이 평형을 이루는 추의 배치 방법 각각에 대해 최대 10자리의 정수가 하나씩 대응된다. 이 수를 “평형정수“라고 하자.
주어진 추 집합을 입력으로 받아서 생성할 수 있는 모든 평형정수를 증가하는 순서대로 놓았을 때 k번째에 해당되는 평형정수를 출력하는 프로그램을 작성하라. 0≤k≤1,000,000,000 이다. 특수한 경우로 k=0 에 대응되는 평형정수는 0으로 저울의 양쪽에 아무 추도 놓이지 않은 상태를 말한다. 만일 k번째에 해당하는 평형정수가 없으면 가능한 가장 큰 평형정수를 출력한다.