문제2.
경비행기 독수리호가 출발지 S에서 목적지 T로 가능한 빠른 속도로 안전하게 이동하고자 한다. 이때, 경비행기의 연료통의 크기를 정하는 것이 중요한 문제가 된다. 큰 연료통을 장착하면 중간에 내려서 급유를 받는 횟수가 적은 장점이 있지만 연료통의 무게로 인하여 속도가 느려지고, 안정성에도 문제가 있을 수 있다. 한편 작은 연료통을 장착하면 비행기의 속도가 빨라지는 장점이 있지만 중간에 내려서 급유를 받아야 하는 횟수가 많아지는 단점이 있다. 문제는 중간에 내려서 급유를 받는 횟수가 k이하 일 때 연료통의 최소용량을 구하는 것이다. 아래 예를 보자.
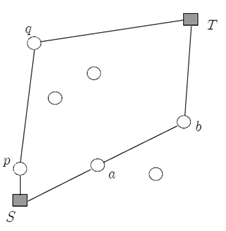
위 그림은 S, T와 7개의 중간 비행장의 위치를 나타내고 있는 그림이다. 위 예제에서 중간급유를 위한 착륙 허용 최대횟수 k=2라면 S-a-b-T로 가는 항로가 S-p-q-T로 가는 항로 보다 연료통이 작게 된다. 왜냐하면, S-p-q-T항로에서 q-T의 길이가 매우 길어서 이 구간을 위해서 상당히 큰 연료통이 필요하기 때문이다. 문제는 이와 같이 중간에 최대 K번 내려서 갈 수 있을 때 최소 연료통의 크기가 얼마인지를 결정하여 출력하면 된다. 참고사항은 다음과 같다.
a) 모든 비행기는 두 지점 사이를 반드시 직선으로 날아간다. 거리의 단위는 ㎞이고 연료의 단위는 ℓ(리터)이다. 1ℓ당 비행거리는 10㎞이고 연료주입은 ℓ단위로 한다.
b) 두 위치간의 거리는 평면상의 거리이다. 예를 들면, 두 점 g=(2,1)와 h=(37,43)간의 거리 d(g,h)는 
이고 50＜d(g,h)≤60이므로 필요한 연료는 6ℓ가 된다.
c) 출발지 S의 좌표는 항상 (0,0)이고 목적지 T의 좌표는 (10000,10000)으로 모든 입력 데이터에서 고정되어 있다.
d) 출발지와 목적지를 제외한 비행장의 수 n은 3≤n≤1000이고 그 좌표 값 (x,y)의 범위는 0＜x,y＜10000의 정수이다. 그리고 최대 허용 중간급유 횟수 k는 0≤k≤1000이다.