간선(혹은 에지)에 가중치가 주어진 그래프가 있다. 정점들의 수가 N일 때, 모든 정점은 1부터 N까지 번호가 붙여져 있고, 모든 간선들의 가중치는 서로 다르다.

이 때 서로 다른 두 정점 u,v에 대하여, Cost(u,v)는 다음에서 제거되는 간선들의 가중치 합이다:

u와 v사이의 경로가 있으면 이 그래프의 최소 가중치 간선을 그래프에서 제거한다. 이 과정을 u와 v사이의 경로가 없을 때까지 반복한다.

  예를 들어, 6개의 정점으로 이루어진 다음 그래프를 고려해 보자.

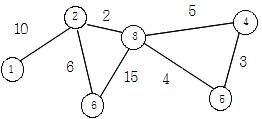
두 정점 2, 6에 대하여, Cost(2,6)을 구하는 과정에서 제거되는 간선들을 차례대로 나열하면 다음과 같다: (2, 3), (4, 5), (3, 5), (3, 4), (2, 6).

이들 간선들 중 (2, 6)이 제거될 때, 두 정점 2와 6사이의 경로가 없으므로 간선 제거가 끝나게 된다. 따라서 Cost(2,6) = 2 + 3 + 4 + 5 + 6 = 20이다.

간선에 가중치가 있는 그래프가 주어질 때, u<v인 모든 두 정점 u,v에 대한 Cost(u,v)들의 총 합을 구하는 프로그램을 작성하시오.

총 합이 10⁹보다 크면 이를 10⁹으로 나눈 나머지를 출력한다.

첫 번째 줄에 정점의 수 N(1<=N<=100,000)과 간선의 수 M(1<=M<=100,000)이 빈칸을 사이에 두고 주어진다. 다음 M개의 각 줄에 간선 하나에 대한 정보를 나타내는 세 개의 양의 정수 x,y,w가 빈칸을 사이에 두고 주어진다. 이는 간선(x,y) 의 가중치가 w임을 의미한다. 이다.

1<=w<=100,000

u<v인 모든 두 정점 u,v에 대한 Cost(u,v)들의 총 합을 첫째 줄에 출력한다. 단, 총 합이 10⁹보다 크면 이를 10⁹으로 나눈 나머지를 출력한다.

전체 테스트 데이터의 20%는 N,M<=100

전체 테스트 데이터의 50%는 N,M<=10,000